너무 큰 데이터: 과다 플로팅에 대처하기

최근 몇 년 동안 빅 데이터에 대한 모든 과대 광고로 인해 더 많은 데이터를 보유하는 것이 항상 이점이라고 가정하기 쉽습니다. 그러나 산점도에 점점 더 많은 데이터 포인트를 추가하면 이러한 패턴과 클러스터가 손실되기 시작할 수 있습니다. 오버플로팅의 결과인 이 문제는 아래 애니메이션에 나와 있습니다.

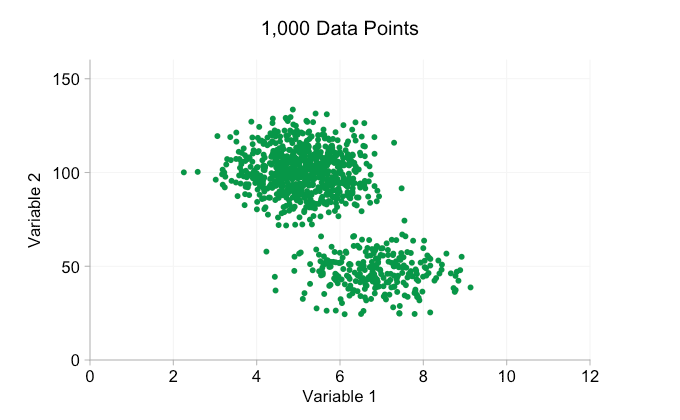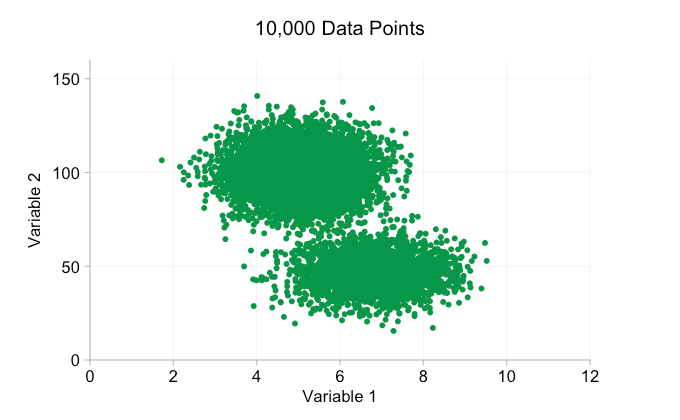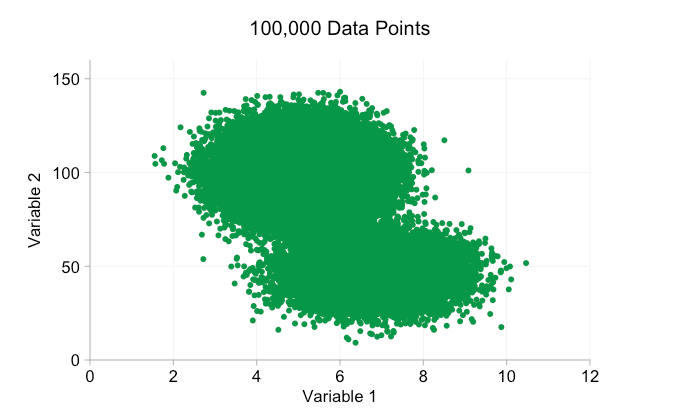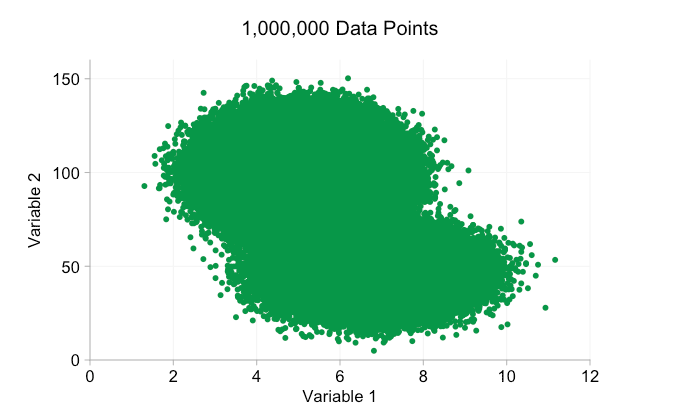
위 애니메이션의 데이터는 한 쌍의 단순 이변량 분포에서 무작위로 생성됩니다. 두 분포 간의 차이는 점점 더 많은 데이터를 추가함에 따라 점점 더 명확해지지 않습니다. 그렇다면 오버플롯에 대해 무엇을 할 수 있습니까?

한 가지 간단한 옵션은 데이터 포인트를 더 작게 만드는 것입니다. (많은 데이터 포인트가 정확히 동일한 값을 공유하는 경우 이는 좋지 않은 "솔루션"입니다.) 우리는 또한 그것들을 반투명하게 만들 수 있습니다. 그리고 다음 두 가지 옵션을 결합할 수 있습니다.

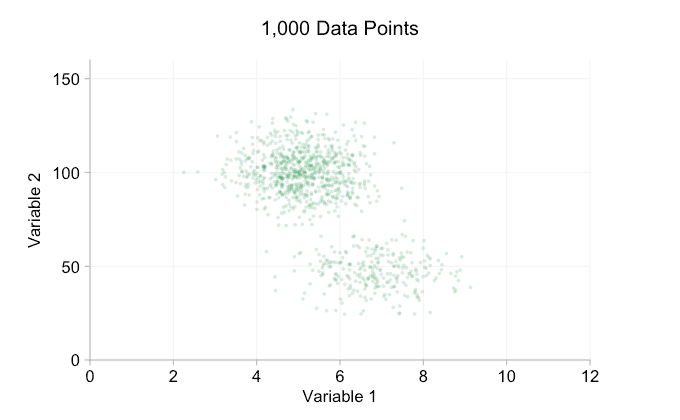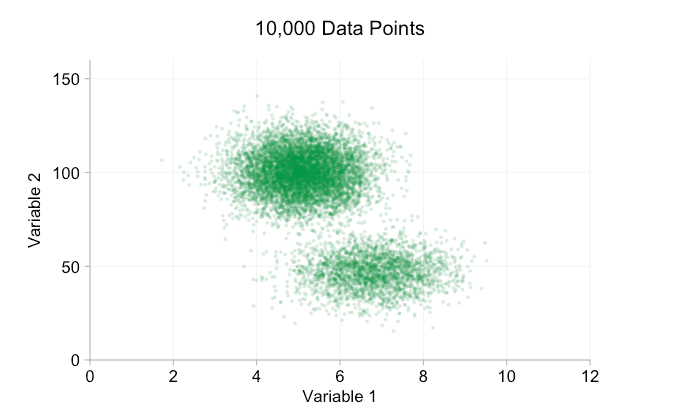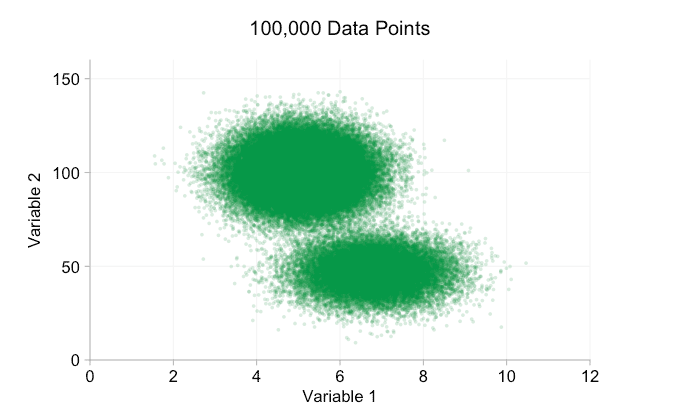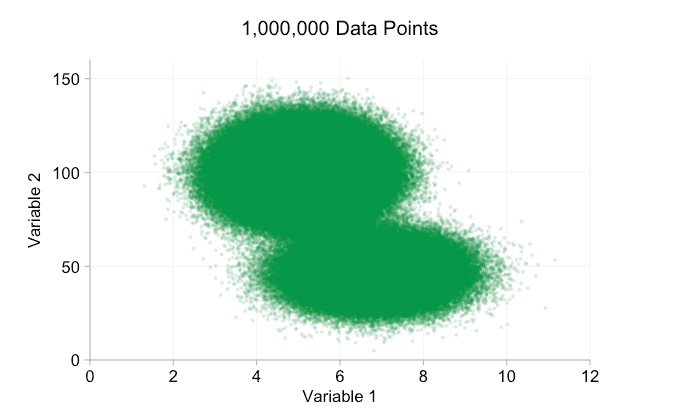
이러한 개선은 10,000개의 데이터 포인트가 있을 때 확실히 도움이 됩니다. 그러나 100만 포인트에 도달할 때쯤에는 두 분포가 다시 하나로 합쳐진 것처럼 보입니다. 요점을 더 작고 투명하게 만들면 도움이 될 수 있습니다. 그럼에도 불구하고 어느 시점에서는 시각화의 변경을 고려해야 할 수도 있습니다. 나중에 다루겠습니다. 하지만 먼저 몇 가지 추가 정보로 시각화를 보완해 보겠습니다. 구체적으로 주변 분포를 시각화해 보겠습니다. 몇 가지 옵션이 있습니다. 러그 플롯에 대한 데이터가 너무 많지만 데이터를 구간화하고 히스토그램을 표시할 수 있습니다. 또는 더 부드러운 옵션인 커널 밀도 플롯을 사용할 수 있습니다. 마지막으로, 경험적 누적 분포를 사용할 수 있습니다. 이 마지막 옵션은 비닝 또는 스무딩을 방지하지만 결과는 덜 직관적일 수 있습니다. 여기서는 커널 밀도 옵션을 사용하겠지만 히스토그램을 선호할 수도 있습니다. 아래의 애니메이션 gif는 위의 gif와 동일하지만 부드러운 여백 분포가 추가되었습니다. 나는 혼란을 피하기 위해 저울을 생략했으며 우리는 상대적인 높이에 대한 대략적인 판단에만 관심이 있기 때문입니다.

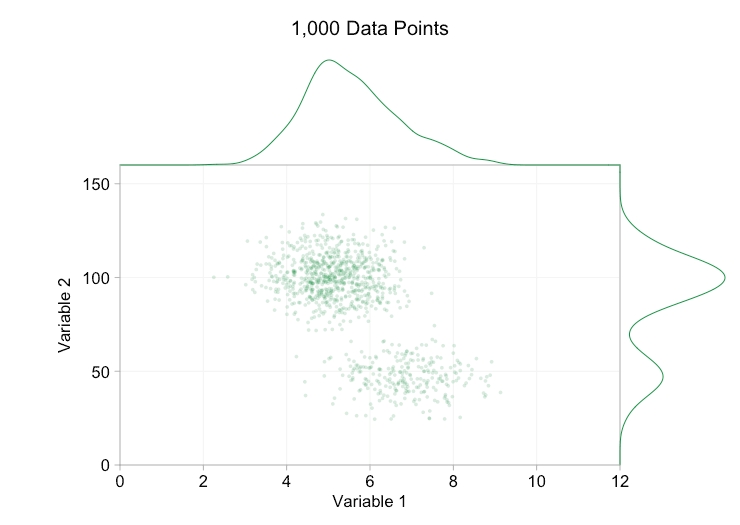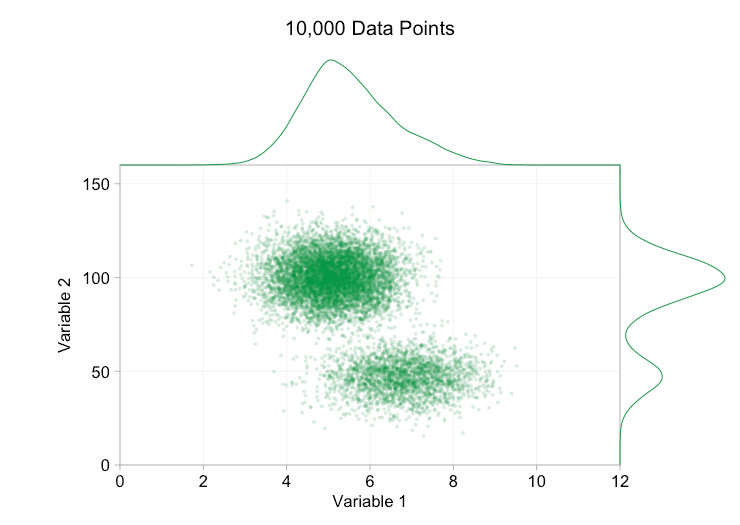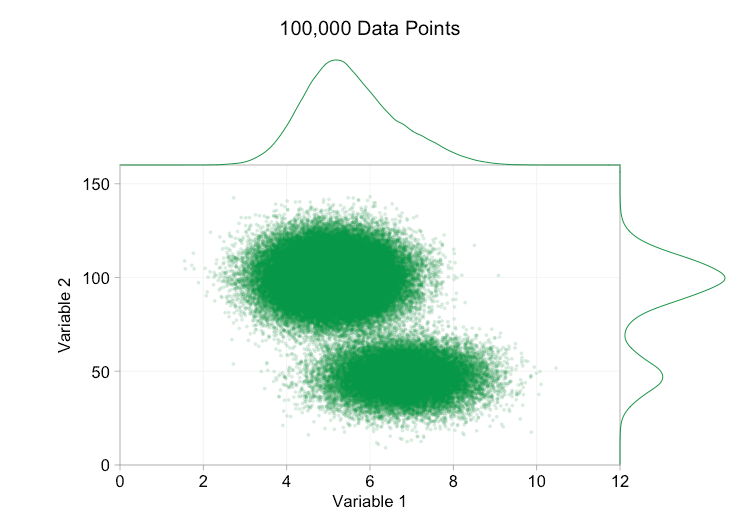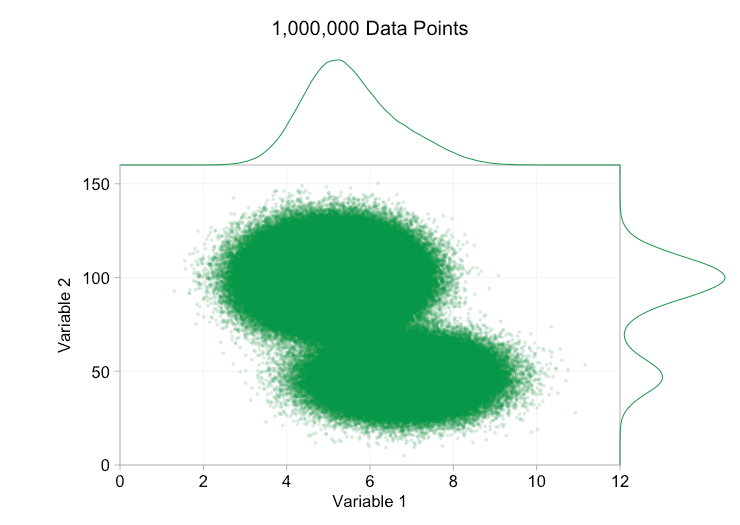
주변 분포, 특히 변수 2의 분포를 추가하면 이변량 데이터에 두 개의 서로 다른 분포가 존재한다는 것을 명확히 하는 데 도움이 됩니다. 변수 2의 트윈 피크 특성은 데이터 포인트가 1,000개인지 100만 개인지에 관계없이 분명합니다. 두 구성 요소의 상대적인 크기도 명확합니다. 반면, 변수 1의 주변 분포는 두 개의 서로 다른 분포에서 왔음에도 불구하고 단일 피크만 있습니다. 이것은 주변 분포를 추가하는 것이 산점도에서 과다 표시에 대한 보편적인 해결책이 아니라는 것을 분명히 해야 합니다. 이 점을 강화하기 위해 아래 애니메이션은 주변 분포가 있는 산점도에서 완전히 다른 (생성된) 데이터 포인트 집합을 보여줍니다. 이 데이터는 다시 두 개의 서로 다른 2D 분포의 무작위 표본에서 추출되지만, 전체 데이터 세트의 두 주변 분포 모두 이러한 분리를 강조하지 못합니다. 이전과 마찬가지로 데이터 포인트의 수가 많으면 산점도에서도 두 클러스터 간의 차이를 볼 수 없습니다.

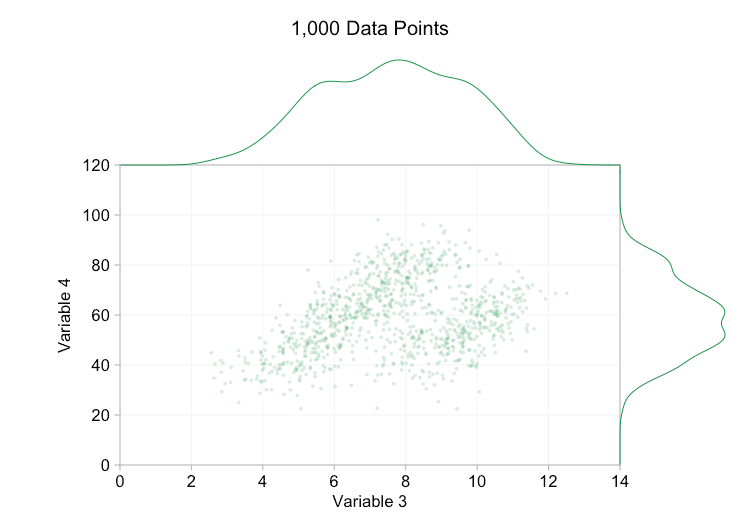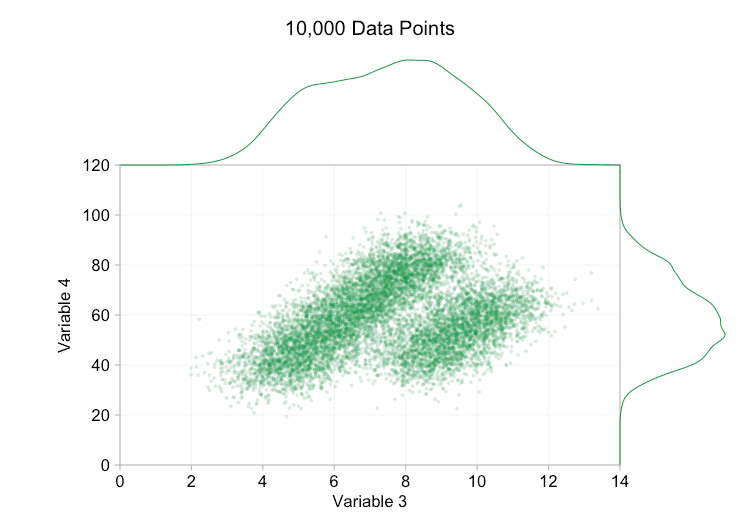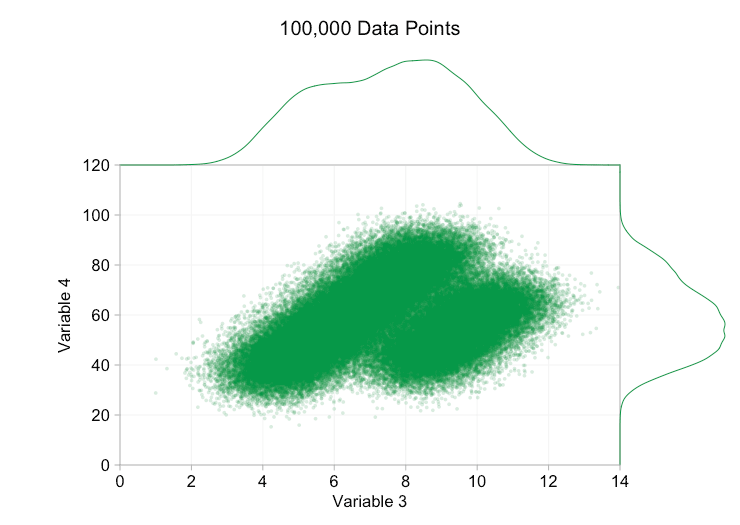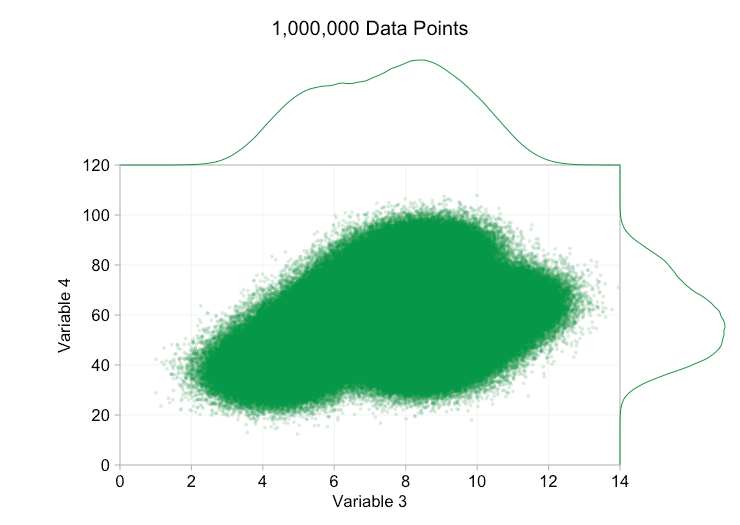
포인트 크기와 불투명도로 돌아가서 데이터 포인트를 매우 작고 거의 완전히 투명하게 만들면 무엇을 얻을 수 있습니까?

이제 각 데이터 세트에서 두 개의 클러스터를 명확하게 구별할 수 있습니다. 하지만 세세한 부분을 파악하기는 어렵습니다.

어쨌든 우리는 그 미세한 세부 사항을 잃어버렸기 때문에 정말 백만 개의 데이터 포인트를 뽑고 싶은지 의문을 제기하는 것이 적절해 보입니다. 특정 상황에서는 지루할 정도로 느리고 불가능할 수 있습니다. 2D 히스토그램이 대안입니다. 데이터를 범주화하면 표시할 점의 수를 줄일 수 있으며, 적절한 색상 척도를 선택하면 산점도의 혼란에서 손실된 일부 기능을 선택할 수 있습니다. 몇 가지 실험을 한 후 검정색에서 녹색, 고급형의 흰색에 이르는 색상 척도를 선택했습니다. 이것은 위의 산점도에서 오버 플로팅으로 생성 된 효과의 (거의) 반대입니다.

두 2D 히스토그램 모두에서 데이터가 추출되는 두 개의 분포를 나타내는 두 개의 서로 다른 클러스터를 명확하게 볼 수 있습니다. 첫 번째 경우에는 오른쪽 아래 클러스터보다 왼쪽 위 클러스터에서 더 많은 카운트가 있음을 볼 수 있으며, 이는 백만 개의 데이터 포인트가 있는 산점도에서 손실된 세부 정보입니다(그러나 주변 분포에서 더 분명함). 반대로, 두 번째 데이터 세트의 경우 두 클러스터의 "높이"가 대략적으로 비슷하다는 것을 알 수 있습니다.

3D 차트는 과도하게 사용되지만 여기(아래 참조)는 데이터가 집중되어 있는 위치와 집중되지 않은 위치에 대한 광범위한 그림을 제공한다는 측면에서 실제로 매우 잘 작동한다고 생각합니다. 기능 폐색은 3D 차트의 문제이므로 자신의 데이터를 탐색할 때 이 경로를 사용하려는 경우 회전 및 확대/축소를 통해 사용자 상호 작용을 허용하는 소프트웨어를 사용하는 것이 좋습니다.

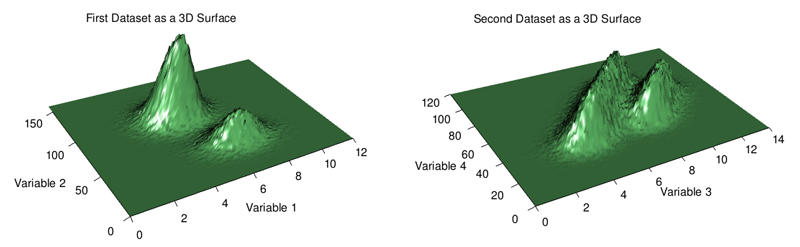
요약하면, 산점도는 이변량 데이터를 시각화하는 간단하고 효과적인 방법입니다. 그러나 차트에 과도한 플로팅이 발생하는 경우 포인트 크기와 불투명도를 줄여 보십시오. 그렇지 않으면 2D 히스토그램 또는 3D 표면 플롯이 도움이 될 수 있습니다. 후자의 경우 오클루전을 조심해야 합니다.