표본 크기에 대한 시각적 탐색

작은 표본을 기반으로 결론을 도출하는 것은 분명히 문제가 있습니다. 동시에 "빅 데이터"의 중요성이 높아짐에 따라 조직이 필요한 분석 작업을 수행하는 데 실제로 얼마나 많은 데이터가 필요한지에 대해 논리적으로 생각하기보다는 맹목적으로 가능한 한 많은 데이터를 수집하게 될 수 있는지 궁금합니다.

충분하지 않은 것보다는 필요한 것보다 조금 더 많은 데이터를 가지고 싶지만, 그렇다고 해서 우리가 할 수 있다고 해서 모든 것을 수집해야 한다는 의미는 아닙니다. 우리는 통계를 사용하여 실제로 얼마나 많은 데이터가 필요한지 안내할 수 있지만, 최근에는 표본 크기를 늘리는 것이 어떤 영향을 미치는지 시각적으로 보여줄 수 있는 방법에 대해 생각하게 되었습니다.

간단하게 하기 위해 정규 분포의 특정(그러나 다소 임의적인) 인스턴스에서 무작위 변수로 표본 크기를 늘리는 효과를 살펴보겠습니다. 매개변수(실제 평균과 실제 표준 편차)에 대한 설명은 나중으로 미루겠습니다.

아래 애니메이션 gif는 앞서 언급한 정규 분포를 샘플링하여 만든 확률 밀도 히스토그램을 보여줍니다. 프레임에서 프레임으로 표본 크기가 10배 증가하고 각 히스토그램을 그리는 데 사용되는 데이터는 이전 프레임에 있는 데이터의 상위 집합이 됩니다. 빨간색 곡선은 표본 데이터와 평균 및 표준 편차가 같은 정규 분포입니다.

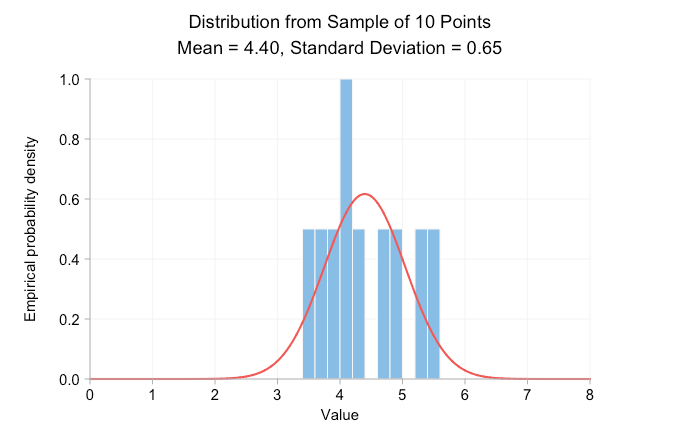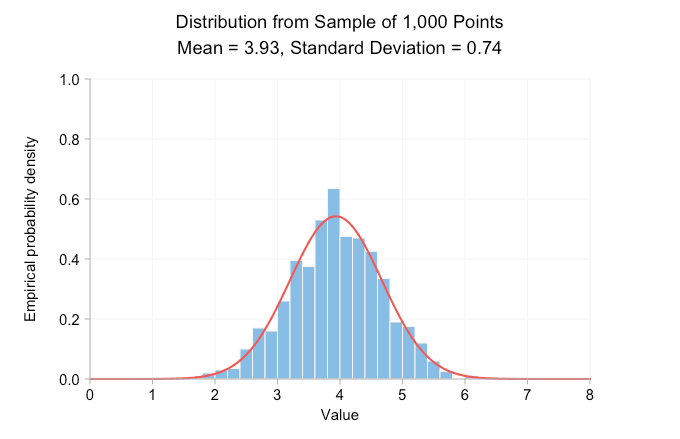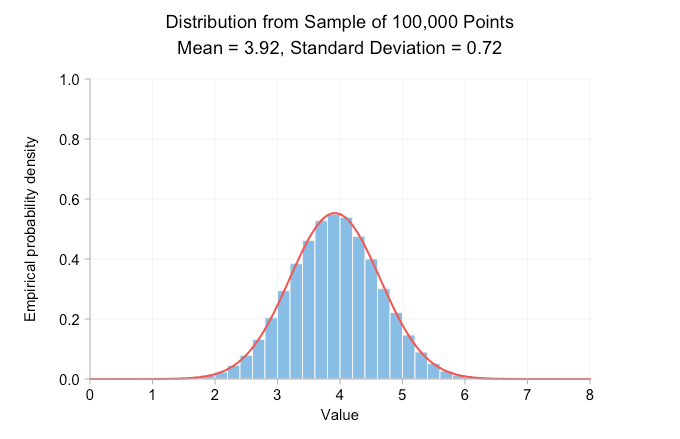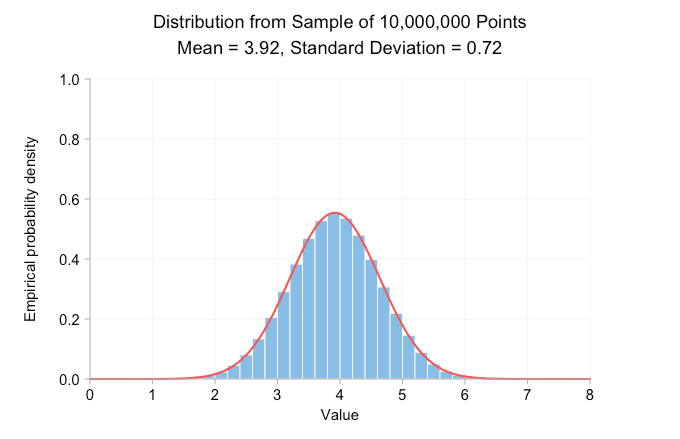
분명히, 표본 크기가 10에 불과하면 경험적 분포는 평균과 표준 편차가 동일한 정규 분포와 전혀 다르게 보입니다. 이것으로부터 우리가 실제로 말할 수 있는 것은 실제 평균이 4 또는 5에 가까울 가능성이 높다는 것입니다. 그러나 표본을 100포인트로 늘리면 이미 대략적인 종형 곡선을 볼 수 있습니다. 100,000포인트에 도달할 때쯤이면 히스토그램과 곡선이 시각적으로 매우 잘 일치합니다. 점을 더 추가해도 분포의 모양이나 인쇄된 평균 및 표준 편차는 변경되지 않습니다.

애니메이션 히스토그램은 더 많은 포인트를 추가함에 따라 상황이 어떻게 변하는지에 대한 광범위한 개요를 제공하는 데 적합하지만 10의 모든 요소에 대해 하나의 프레임만 있기 때문에 매우 상세한 그림을 볼 수 없습니다. 맨 위에 있는 제목의 매개변수에 더 많은 숫자를 인쇄하지 않으면 특정 표본 크기에 대한 평균과 표준 편차를 얼마나 정확하게 알 수 있는지 명확하지 않습니다. 이에 대한 더 나은 아이디어를 위해 매개변수를 선택하고 이를 표본 크기의 함수로 2점(두 표본 매개변수가 모두 유한한 경우)에서 최대 1,000만 개까지 표시할 수 있습니다. 먼저 평균을 살펴보겠습니다.

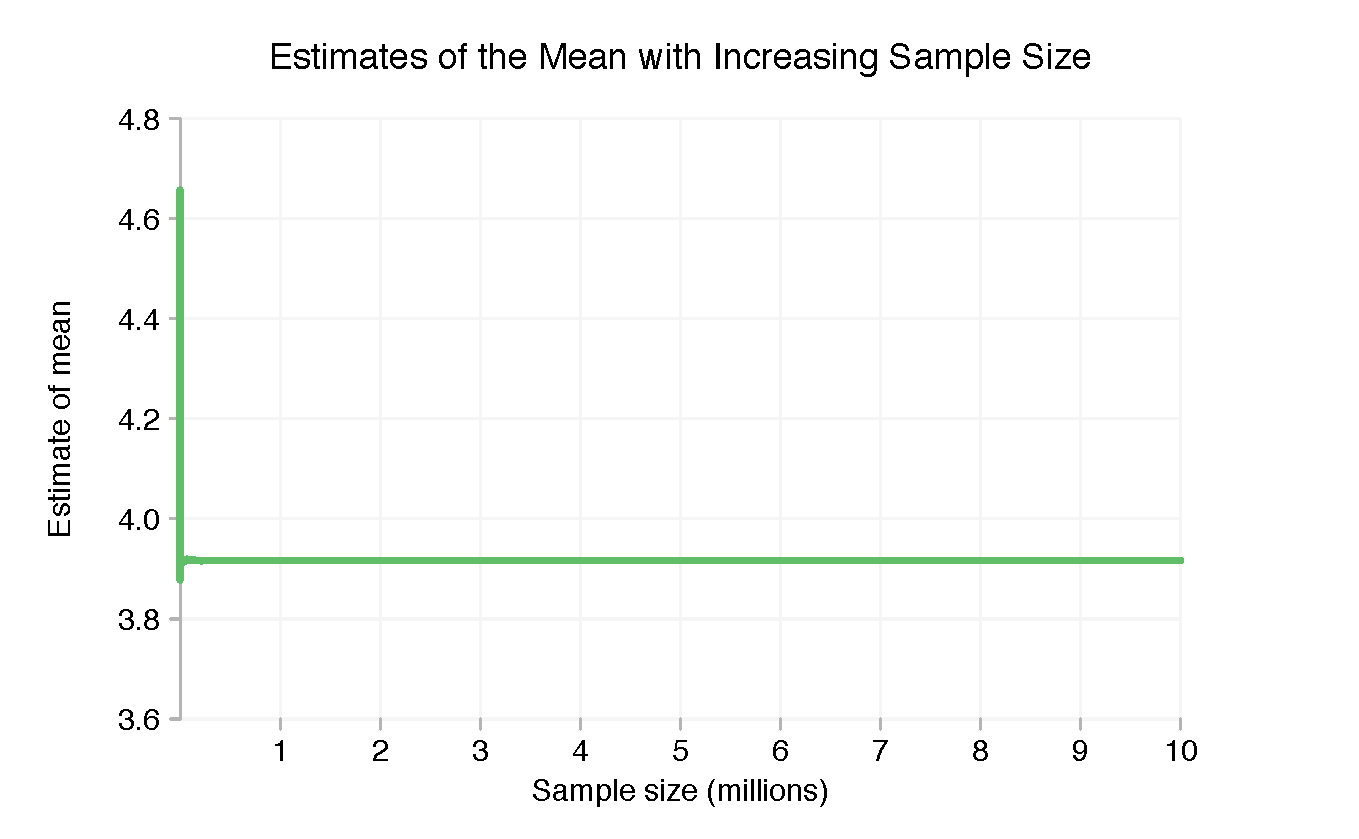
적은 양의 데이터만 있을 때 상황이 훨씬 더 빨리 변하기 때문에 위의 차트는 거의 쓸모가 없습니다. 샘플의 포인트 수에 대한 (기본 10) 로그를 취하면 상황이 훨씬 더 명확해집니다.

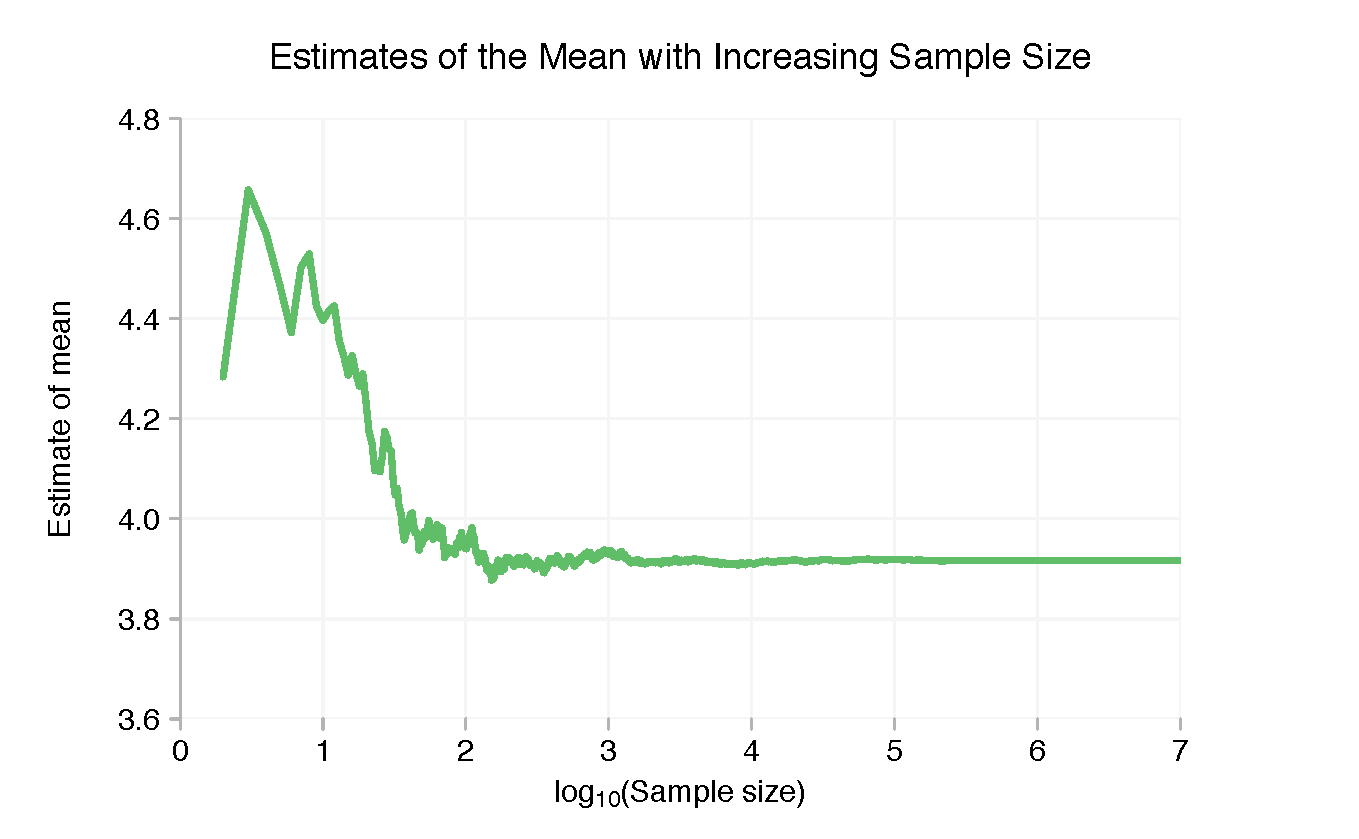
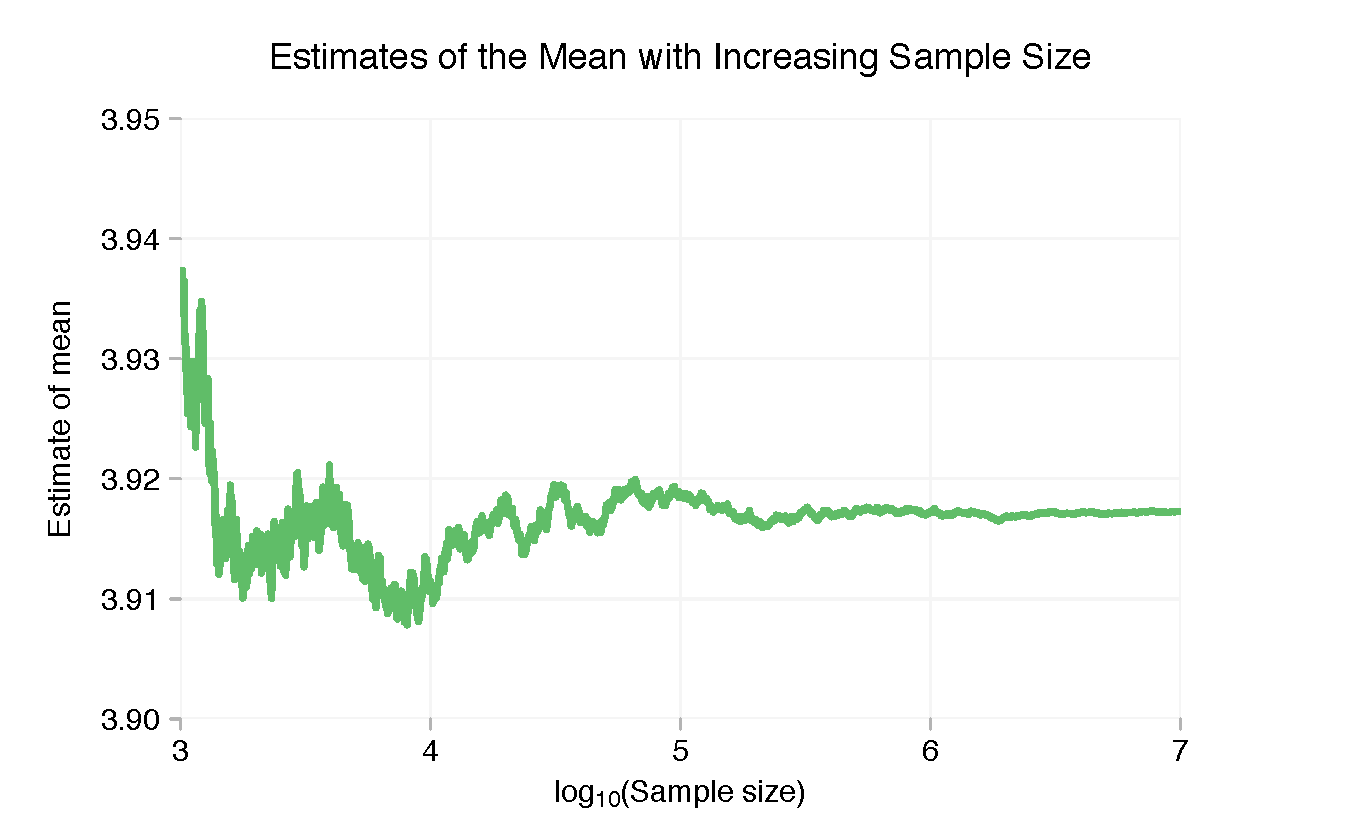
점이 몇 개뿐인 경우 표본 평균이 4보다 훨씬 높습니다. 그러나 이것은 빠르게 떨어지고 두 자릿수에 들어가면 안정화됩니다. 수천 포인트를 넘어서면 표본 평균에 눈에 띄는 변동이 거의 없지만 오른쪽을 확대하면 더 미세한 "흔들림"을 볼 수 있습니다.

표본 크기를 변경함에 따라 표준 편차가 어떻게 변하는지 보여줍니다(참고: 이것은 평균의 표준 오차가 아니라 표본의 표준 편차 입니다!).

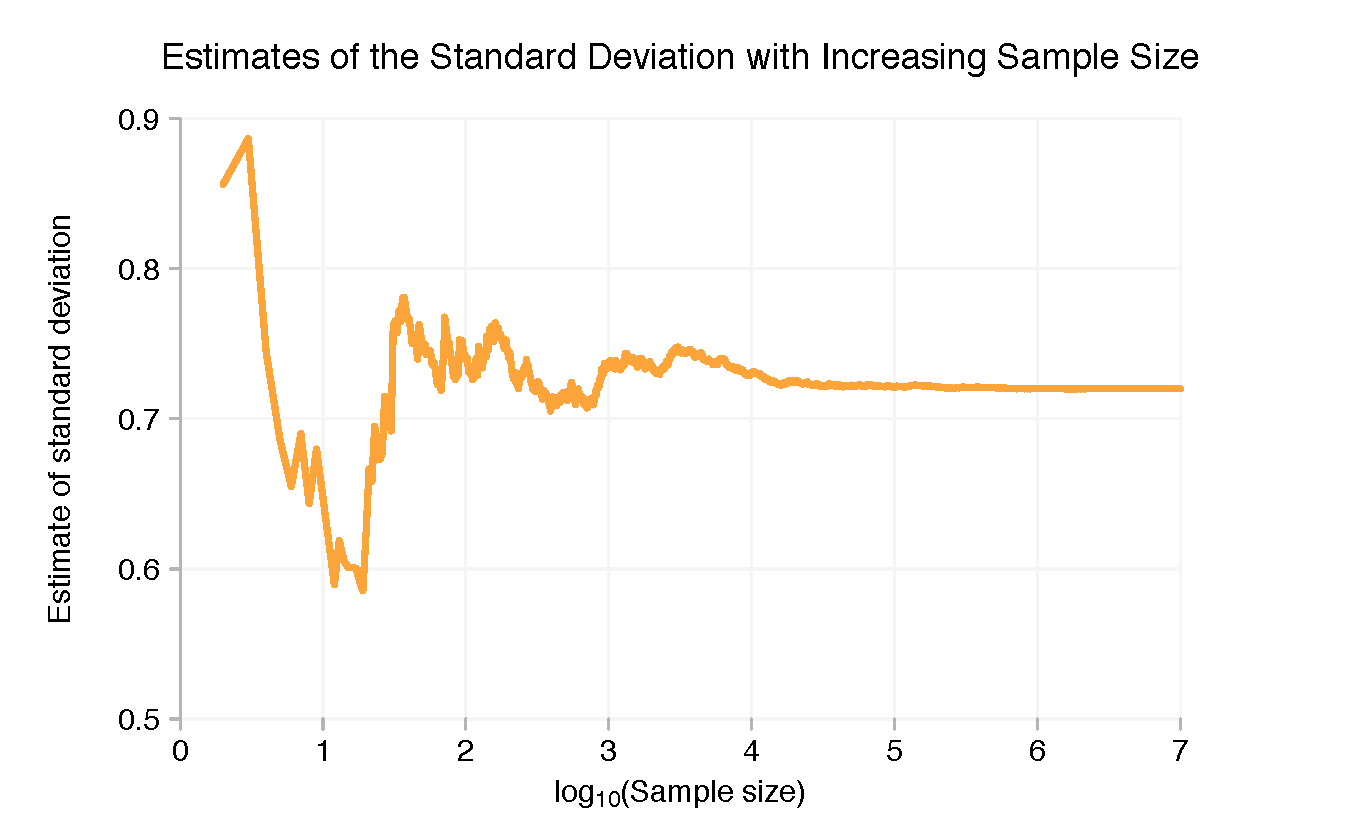
표본을 생성하는 데 사용된 실제 평균은 3.9172이고 표준 편차는 0.7200이었습니다. 차트에서 볼 수 있듯이 엄격한 통계 분석 없이 천만 개의 데이터 포인트가 있는 이 수치에 매우 근접해 있습니다. 하지만 1만 개의 데이터 포인트에서도 그리 멀리 떨어져 있지 않았습니다. 데이터가 많을수록 정밀도가 높아지지만, 평균이 4보다 크거나 작은지 여부만 알면 ~1,000포인트면 충분했을 것입니다.

요점을 강화하기 위해 처음 100,000개의 데이터 포인트만 살펴보고 이를 10,000개씩 10개의 샘플로 나눕니다. 각 하위 샘플에서 이전과 동일한 그래픽 기술을 사용할 수 있습니다. 아래 차트의 색상이 지정된 선은 처음 10,000개의 데이터 점에 대한 결과를 보여주고, 회색 선은 다른 하위 샘플에 대한 결과를 보여줍니다.

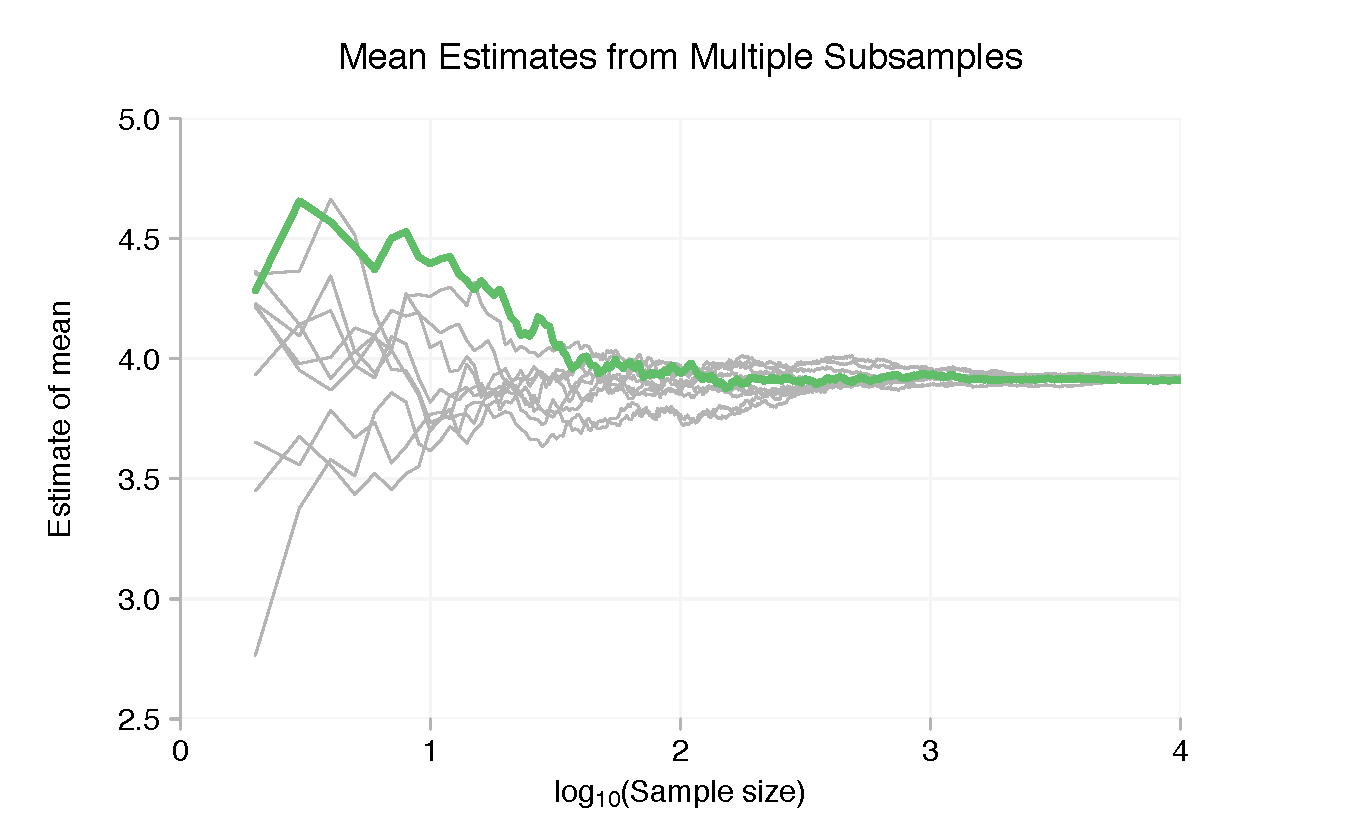
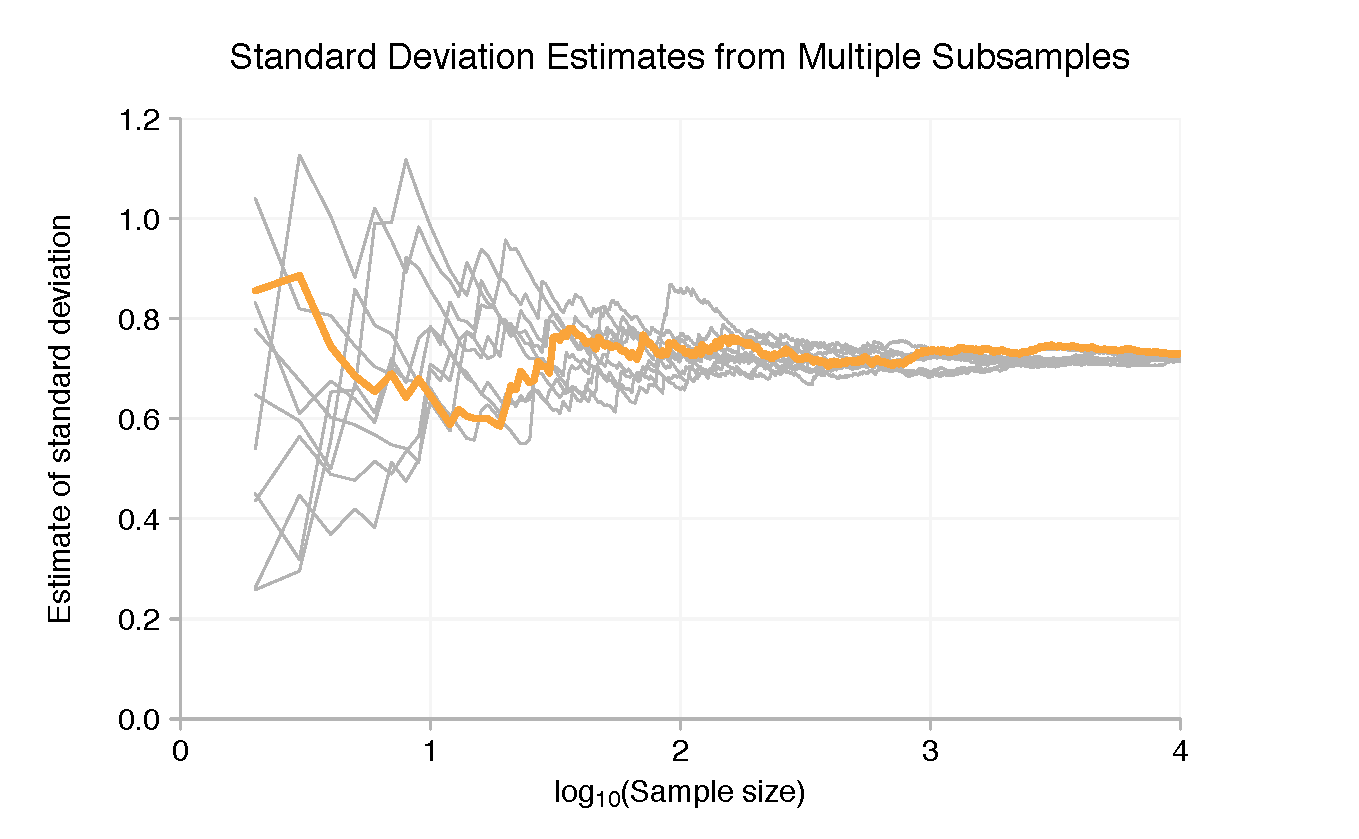
분명히 말하자면, 차트의 목적은 실제로 하나의 하위 샘플에 의해 만들어진 개별 트랙을 보는 것이 아닙니다. 이는 하위 표본의 평균과 표준 편차가 각 샘플에 데이터 포인트가 몇 개만 있을 때 널리 퍼져 있지만 적어도 로그 스케일에서는 더 많은 포인트를 추가함에 따라 빠르게 수렴한다는 것을 보여주기 위한 것입니다.

물론 모든 데이터 세트는 다르며 많은 데이터 세트가 단순한 무작위 샘플링을 통해 생성되지 않습니다. 또한 실제 데이터 세트가 정규 분포의 단일 인스턴스에서 컴퓨터로 생성된 대규모 랜덤 변수 모음만큼 잘 동작할 것이라고 가정할 수 없습니다. 더욱이, 위의 차트 아이디어는 엄격한 통계 작업을 직접 대체하기 위한 것이 아닙니다. 그러나 어떤 경우에는 예를 들어 통계적 평가에 대한 온전성 검사를 제공하거나 기술적 전문성이 부족한 청중을 위한 시각적 대안으로 이를 보완할 수 있습니다.

단일 라인 코드를 작성하기 전에 빌드가 어떻게 보이고 작동하는지 정확히 확인할 수 있는 포괄적이고 신속한 프로토타이핑 도구를 찾고 계십니까? 더 이상 찾지 마십시오. 지금 Indigo Studio 무료 평가판을 다운로드하여무엇을 할 수 있는지 확인하십시오!